Credible interval

Bayesian statistics
Theory
Bayesian probability Probability interpretations Bayes' theorem Bayes' rule · Bayes factor Bayesian inference Bayesian network Prior · Posterior · Likelihood Conjugate prior Hyperparameter · Hyperprior Principle of indifference Principle of maximum entropy Empirical Bayes method Cromwell's rule Bernstein–von Mises theorem Bayesian information criterion Credible interval Maximum a posteriori estimation
Techniques
Bayesian linear regression Bayesian estimator Approximate Bayesian computation

In Bayesian statistics, a credible interval (or Bayesian confidence interval) is an interval in the domain of a posterior probability distribution used for interval estimation^[1]. The generalisation to multivariate problems is the credible region. Credible intervals are analogous to confidence intervals in frequentist statistics^[2].

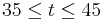For example, in an experiment that determines the uncertainty distribution of parameter $t$ , if the probability that $t$ lies between 35 and 45 is 90%, then $35 \le t \le 45$ is a 90% credible interval.

Choosing a credible interval

Credible intervals are not unique on a posterior distribution. Methods for defining a suitable credible interval include:

Choosing the narrowest interval, which for a unimodal distribution will involve choosing those values of highest probability density including the mode.
Choosing the interval where the probability of being below the interval is as likely as being above it. This interval will include the median.
Assuming the mean exists, choosing the interval for which the mean is the central point.

It is possible to frame the choice of a credible interval within decision theory and, in that context, an optimal interval will always be a highest probability density set.^[3]

Contrasts with confidence interval

A frequentist 90% confidence interval of 35–45 means that with a large number of repeated samples, 90% of the calculated confidence intervals would include the true value of the parameter. The probability that the parameter is inside the given interval (say, 35–45) is either 0 or 1 (the non-random unknown parameter is either there or not). In frequentist terms, the parameter is fixed (cannot be considered to have a distribution of possible values) and the confidence interval is random (as it depends on the random sample). Antelman (1997, p. 375) summarizes a confidence interval as "... one interval generated by a procedure that will give correct intervals 95 % [resp. 90 %] of the time". ^[4]

In general, Bayesian credible intervals do not coincide with frequentist confidence intervals for two reasons:

credible intervals incorporate problem-specific contextual information from the prior distribution whereas confidence intervals are based only on the data;
credible intervals and confidence intervals treat nuisance parameters in radically different ways.

For the case of a single parameter and data that can be summarised in a single sufficient statistic, it can be shown that the credible interval and the confidence interval will coincide if the unknown parameter is a location parameter (i.e. the forward probability function has the form 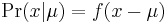$\mathrm{Pr}(x|\mu) = f(x - \mu)$ ), with a prior that is a uniform flat distribution;^[5] and also if the unknown parameter is a scale parameter (i.e. 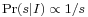the forward probability function has the form $\mathrm{Pr}(x|s) = f(x/s)$ ), with a Jeffreys' prior $\scriptstyle{\mathrm{Pr}(s|I) \;\propto\; 1/s}$ ^[5] — the latter following because taking the logarithm of such a scale parameter turns it into a location parameter with a uniform distribution. But these are distinctly special (albeit important) cases; in general no such equivalence can be made.

References

^ Edwards, W., Lindman, H., Savage, L.J. (1963) "Bayesian statistical inference in statistical research". Psychological Research, 70, 193-242
^ Lee, P.M. (1997) Bayesian Statistics: An Introduction, Arnold. ISBN 0-340-67785-6
^ O'Hagan, A. (1994) Kendall's Advance Theory of Statistics, Vol 2B, Bayesian Inference, Section 2.51. Arnold, ISBN 0-340-52922-9
^ Antelman, G. (1997) Elementary Bayesian Statistics (Madansky, A. & McCulloch, R. eds.). Cheltenham, UK: Edward Elgar ISBN 978-1-85898-504-6
^ ^a ^b Jaynes, E. T. (1976). "Confidence Intervals vs Bayesian Intervals", in Foundations of Probability Theory, Statistical Inference, and Statistical Theories of Science, (W. L. Harper and C. A. Hooker, eds.), Dordrecht: D. Reidel, pp. 175 et seq

Statistics

Descriptive statistics

Continuous data

Location	Mean (Arithmetic, Geometric, Harmonic) Median Mode

Dispersion	Range Standard deviation Coefficient of variation Percentile Interquartile range

Shape	Variance Skewness Kurtosis Moments L-moments

Count data

Index of dispersion

Summary tables

Dependence

Statistical graphics

Data collection

Designing studies	Effect size Standard error Statistical power Sample size determination

Survey methodology	Sampling Stratified sampling Opinion poll Questionnaire

Controlled experiment	Design of experiments Randomized experiment Random assignment Replication Blocking Factorial experiment Optimal design

Uncontrolled studies	Natural experiment Quasi-experiment Observational study

Statistical inference

Statistical theory	Sampling distribution Sufficient statistic Meta-analysis

Bayesian inference	Bayesian probability Prior Posterior Credible interval Bayes factor Bayesian estimator Maximum posterior estimator

Frequentist inference	Confidence interval Hypothesis testing Likelihood-ratio

Specific tests	Z-test (normal) Student's t-test F-test Pearson's chi-squared test Wald test Mann–Whitney U Shapiro–Wilk Signed-rank Kolmogorov–Smirnov test

General estimation	Bias Robustness Efficiency Maximum likelihood Method of moments Minimum distance Density estimation

Correlation and regression analysis

Correlation	Pearson product-moment correlation Partial correlation Confounding variable Coefficient of determination

Regression analysis	Errors and residuals Regression model validation Mixed effects models Simultaneous equations models

Linear regression	Simple linear regression Ordinary least squares General linear model Bayesian regression

Non-standard predictors	Nonlinear regression Nonparametric Semiparametric Isotonic Robust

Generalized linear model	Exponential families Logistic (Bernoulli) Binomial Poisson

Partition of variance	Analysis of variance (ANOVA) Analysis of covariance Multivariate ANOVA Degrees of freedom

Categorical, multivariate, time-series, or survival analysis

Categorical data	Cohen's kappa Contingency table Graphical model Log-linear model McNemar's test

Multivariate statistics	Multivariate regression Principal components Factor analysis Cluster analysis Copulas

Time series analysis	Decomposition (Trend, Stationary process) ARMA model ARIMA model Vector autoregression Spectral density estimation

Survival analysis	Survival function Kaplan–Meier Logrank test Failure rate Proportional hazards models Accelerated failure time model

Applications

Biostatistics	Bioinformatics Biometrics Clinical trials & studies Epidemiology Medical statistics

Engineering statistics	Chemometrics Methods engineering Probabilistic design Process & Quality control Reliability System identification

Social statistics	Actuarial science Census Crime statistics Demography Econometrics National accounts Official statistics Population Psychometrics

Spatial statistics	Cartography Environmental statistics Geographic information system Geostatistics Kriging

Category
Portal
Outline
Index